Fiche de cours

Utiliser des arbres binaires de recherche

Lycée > Terminale > NSI > Utiliser des arbres binaires de recherche

Fiche de cours
Quiz et exercices
Vidéos et podcasts

Objectif

Comprendre et utiliser la structure d’un arbre binaire de recherche.

Points clés

Dans un arbre binaire de recherche, les étiquettes sont appelées des clés.
Dans un arbre binaire de recherche non vide, la racine est supérieure ou égale à toutes les clés de son sous-arbre gauche.
Dans un arbre binaire de recherche non vide, la racine est inférieure à toutes les clés de son sous-arbre droit.
Les sous-arbres d’un arbre binaire de recherche sont des arbres binaires de recherche.

Pour bien comprendre

Comprendre la structure hiérarchique des arbres binaires.
Étudier et implémenter un arbre binaire.

1. L'arbre binaire de recherche

a. Définition d'un ensemble totalement ordonné

Un ensemble totalement ordonné est un ensemble muni d’une relation d’ordre totale.

Une relation d’ordre totale est une relation binaire qui permet de comparer tous les éléments de l’ensemble.

Exemple
L’ensemble des entiers est totalement ordonné car le symbole « plus petit ou égal » ≤ permet de comparer deux à deux tous les nombres entiers.

Par exemple, si on considère les entiers 7 et 3, on peut les « ranger » avec la relation d’ordre ≤ : 3 ≤ 7. On peut faire cela avec tous les couples de nombres entiers.

Attention
La relation binaire < n’est pas une relation d’ordre totale puisqu’on ne peut pas comparer les entiers 4 et 4 : 4 < 4 est faux. En revanche, 4 ≤ 4 est vrai.

b. Principe de l'arbre binaire de recherche

Un arbre binaire de recherche (ou ABR en abrégé) est soit vide, soit c’est un arbre binaire dont les étiquettes sont des éléments d’un ensemble totalement ordonné. On parle ici davantage de clé que d’étiquette.

Un arbre binaire de recherche non vide est défini par trois propriétés.

La clé de la racine est supérieure ou égale à toutes les clés de son sous-arbre gauche.
La clé de la racine est inférieure strictement à toutes les clés de son sous-arbre droit.
Son sous-arbre gauche et son sous-arbre droit sont eux-même des arbres binaires de recherche.

Exemple
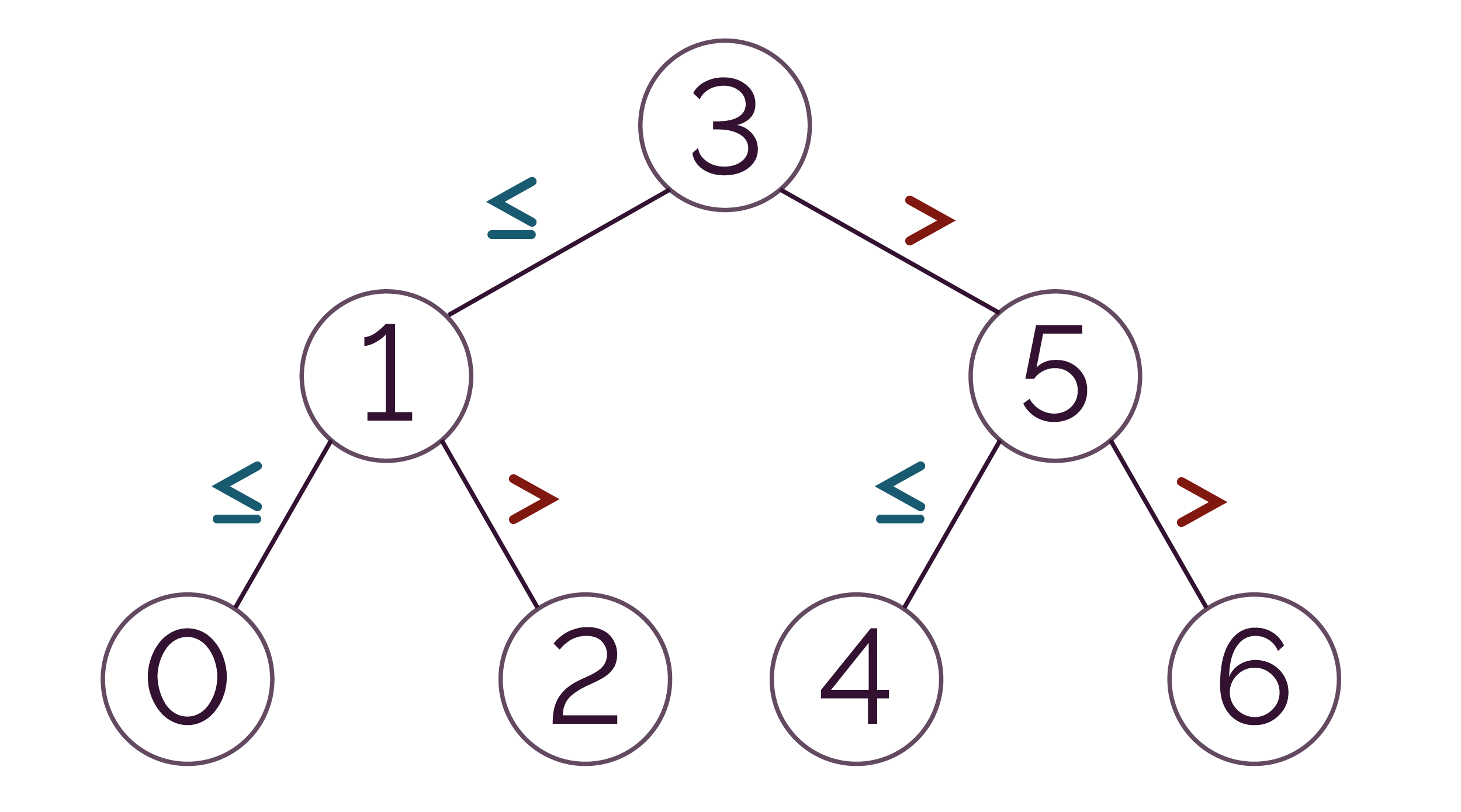
L’arbre suivant est un arbre binaire de recherche.

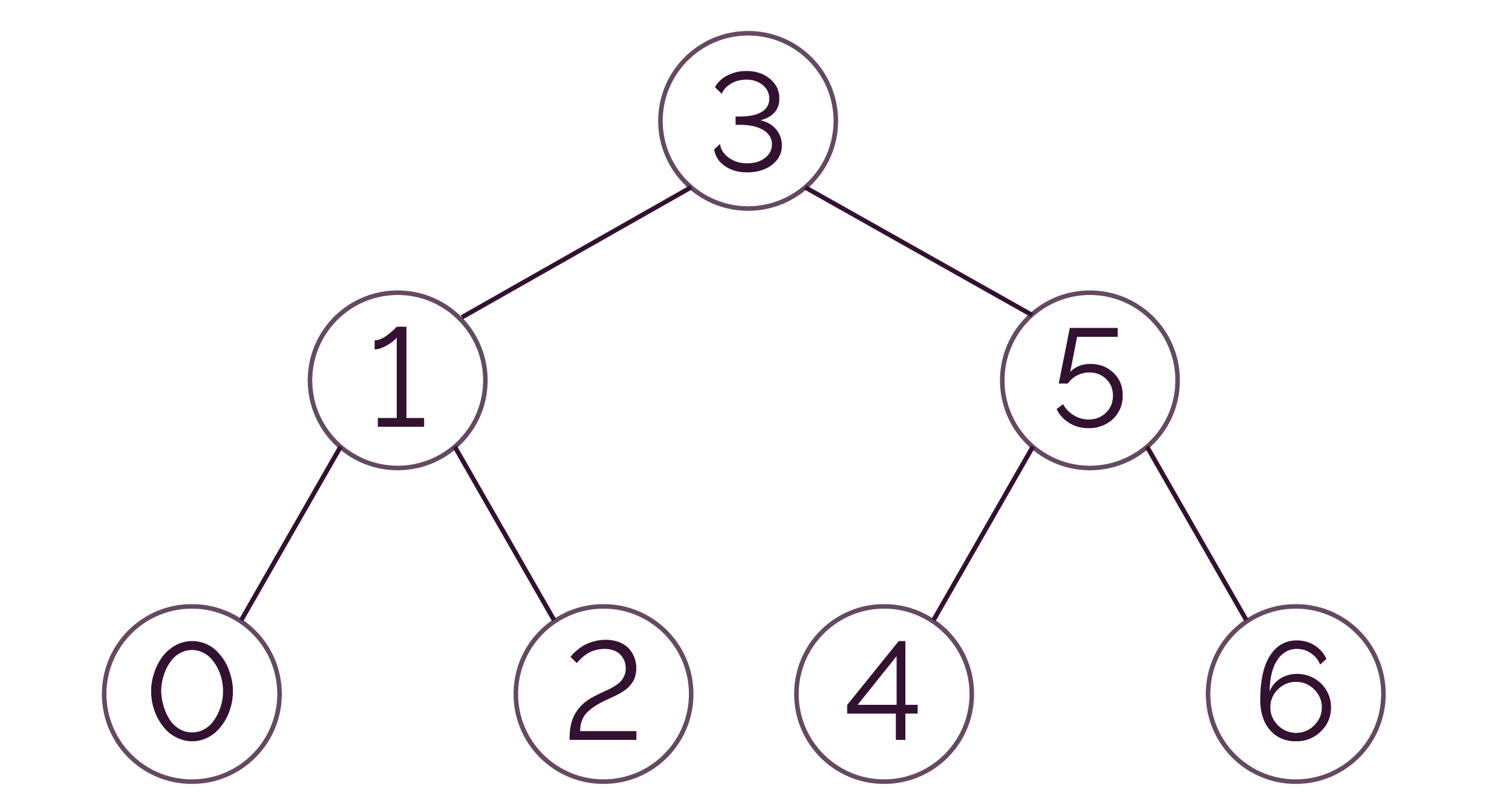
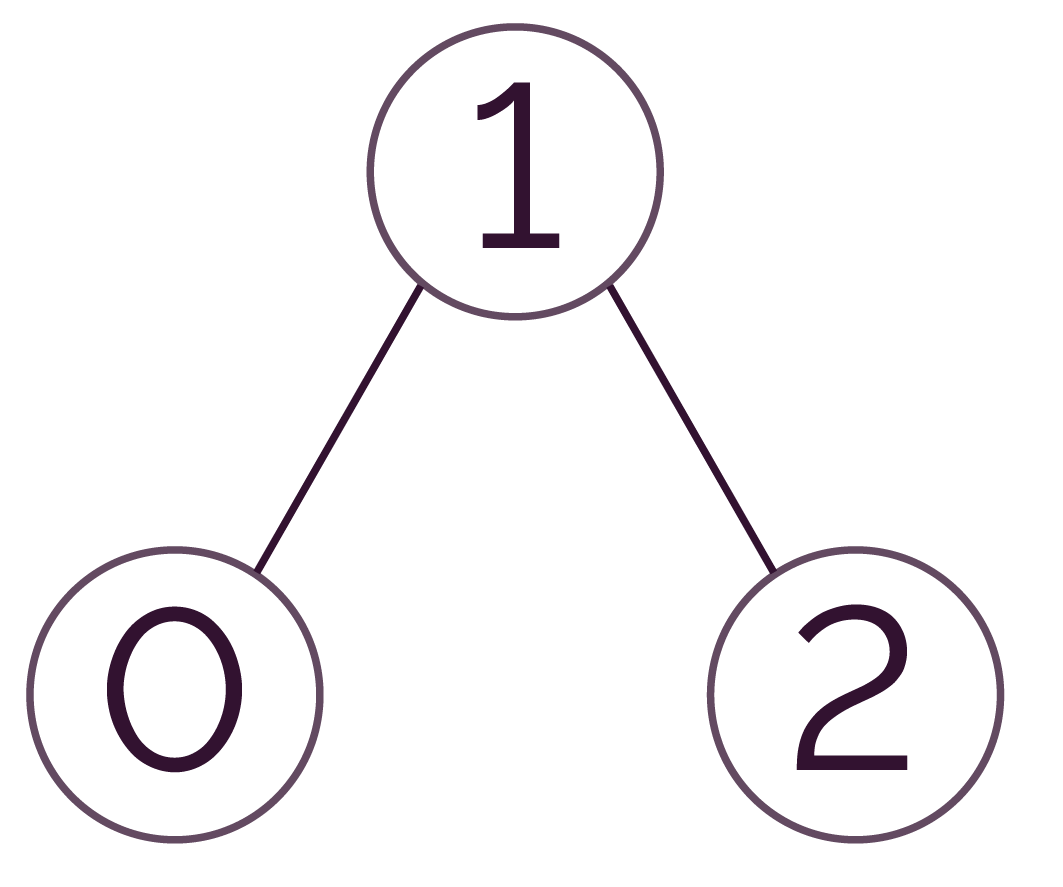
Le sous-arbre gauche de cet arbre est en effet le suivant.

C’est un ABR car la racine est 1 et on a :

à gauche : 0 ≤ racine :
à droite : 2 > racine.

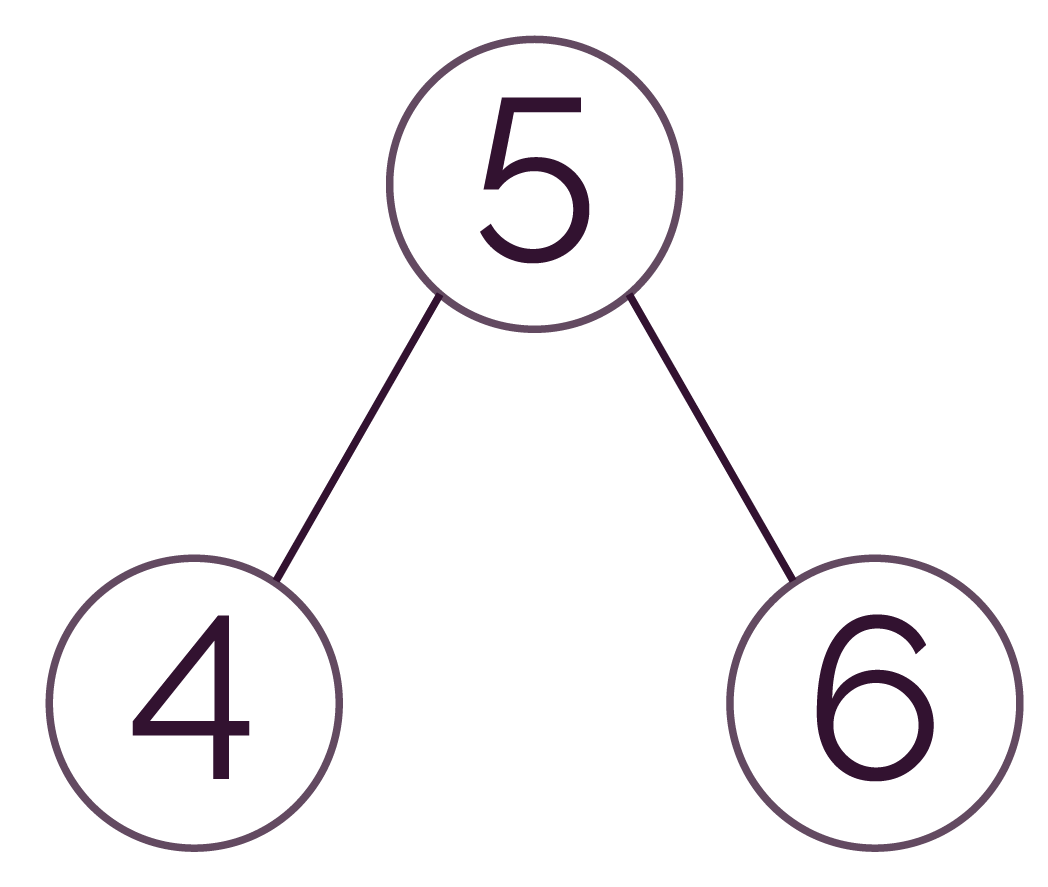
Également, le sous-arbre droit de cet arbre est le suivant.

C’est un ABR car la racine est 5 et on a :

à gauche : 4 ≤ racine ;
à droite : 6 > racine.

Et enfin, si on considère 3, la racine de l’arbre, on a :

à gauche : 1 ≤ racine (le fils gauche de la racine est inférieur ou égal à la racine) ;
à droite : 5 > racine (le fils droit de la racine est supérieur à la racine).

On peut représenter ces comparaisons sur l’arbre de la manière suivante.

Dans cette représentation, on met les racines à droite des relations binaires ≤ et >, et à gauche leurs fils. Si on considère le sous-ABR ci-dessous, on a ainsi 0 ≤ 1 et 2 > 1.

2. Utiliser des arbres binaires de recherche

a. Généralités

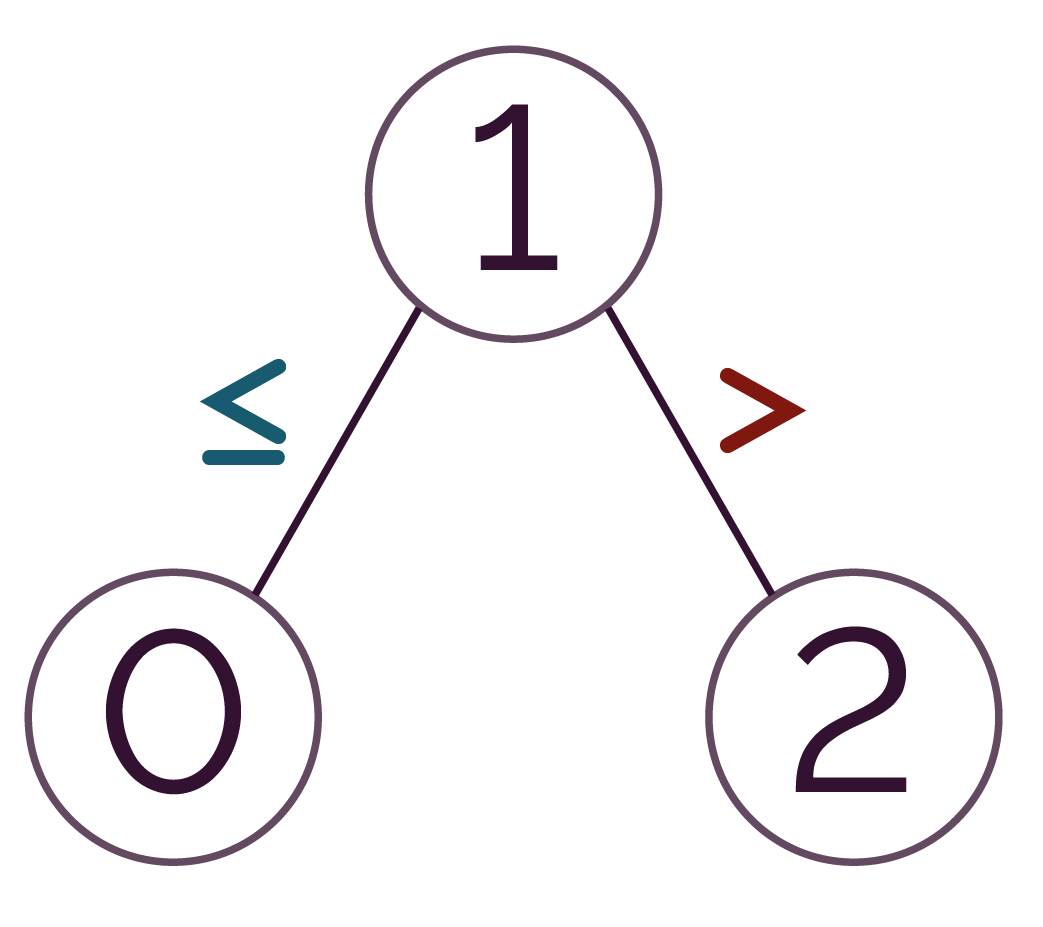
En informatique, la structure d’arbre est très utilisée. Les informations y sont en effet souvent hiérarchisées et peuvent être facilement représentées sous la forme d’arbres.

La structure d’arbre binaire de recherche est idéale puisqu'elle permet de stocker efficacement des données très volumineuses tout en assurant un accès rapide. Lorsque l’on parcourt un arbre binaire de recherche, la relation d’ordre permet en effet, à chaque nœud, de savoir si on parcourt le sous-arbre gauche ou le sous-arbre droit.

Pour un arbre binaire de recherche de hauteur h, un parcours se fera au plus en h comparaisons alors que cet arbre contiendra au plus 2^h – 1 nœuds.

La complexité d’un parcours d’arbre binaire de recherche est logarithmique, elle se note O(ln(h)). C’est bien plus efficace qu’un parcours de structures linéaires (liste, pile, file) qui est linéaire.

b. Recherche d'une clé dans un arbre binaire de recherche

La recherche d’une clé dans un arbre binaire de recherche non vide consiste à comparer la clé et la racine, puis, si elles sont différentes, à descendre dans le sous-arbre gauche ou le sous-arbre droit, selon que la clé est plus petite ou plus grande que la racine. La recherche s’arrête quand on trouve la clé dans l’arbre ou quand on a atteint une feuille.

Exemples
On considère l’arbre binaire de recherche suivant.

On recherche la clé 8 dans cet arbre.

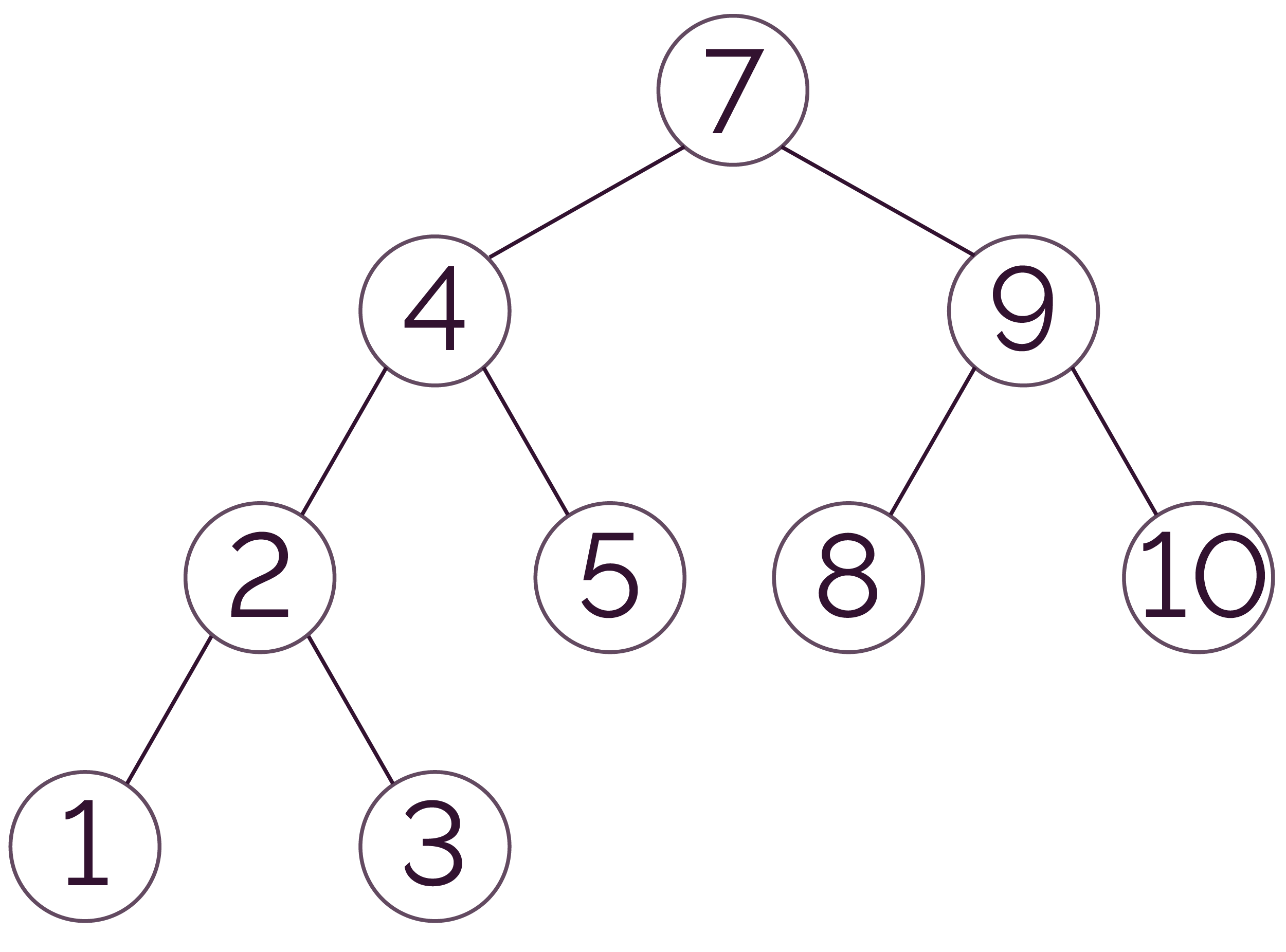
On compare la racine et la clé : 7 < 8.
On cherche donc dans le sous-arbre droit.
On compare la racine du sous-arbre droit et la clé : 9 > 8.
On cherche donc dans le sous-arbre gauche de ce sous-arbre droit.
On compare la racine du sous-arbre gauche du sous-arbre droit et la clé : 8 = 8.
La clé 8 est trouvée !

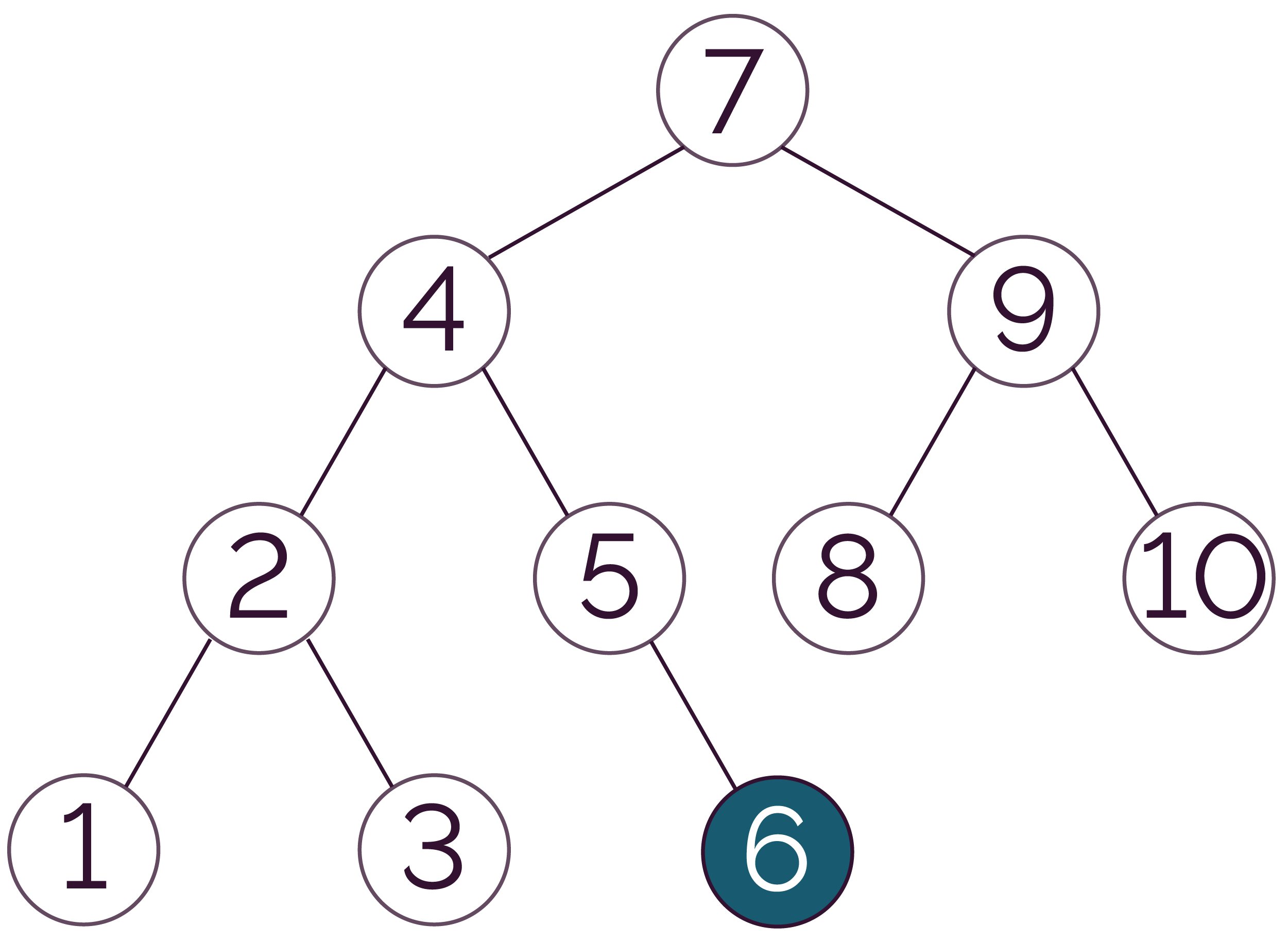
On recherche maintenant la clé 6 dans cet arbre.

On compare la racine et la clé : 7 > 6.
On cherche donc dans le sous-arbre gauche.
On compare la racine du sous-arbre gauche et la clé : 4 < 6.
On cherche donc dans le sous-arbre droit de ce sous-arbre gauche.
On compare la racine du sous-arbre droit du sous-arbre gauche et la clé : 5 < 6.
Or 5 est une feuille, la clé 6 n’est donc pas dans l’arbre.

De manière similaire, ce principe de recherche peut permettre de trouver un nœud dans l’arbre pour y ajouter une clé.

Exemples
On considère à nouveau l’arbre binaire de recherche suivant.

La recherche de la clé 6 s’est arrêtée au nœud 5. On pourrait très bien ajouter 6 au sous-arbre de racine 5, à droite (car la racine est strictement inférieure à cette clé). On aurait ainsi l’arbre suivant.

Évalue ce cours !

Note 4 / 5. Nombre de vote(s) : 2

Des quiz et exercices pour mieux assimiler sa leçon

La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.

S’abonner

Des exercices variés pour ne pas s’ennuyer

Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !

Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.

S’abonner

Des quiz pour une évaluation en direct

Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.

myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.

S’abonner

Des vidéos et des podcasts pour apprendre différemment

Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.

Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !

S’abonner

Des podcasts pour les révisions

La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.

Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.

S’abonner

Des vidéos de cours pour comprendre en image

Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !

S’abonner

Profs en ligne

Découvrez le soutien scolaire en ligne avec myMaxicours

Plongez dans l'univers de myMaxicours et découvrez une approche innovante du soutien scolaire en ligne, conçue pour captiver et éduquer les élèves de CP à la terminale. Notre plateforme se distingue par une riche sélection de contenus interactifs et ludiques, élaborés pour stimuler la concentration et la motivation à travers des parcours d'apprentissage adaptés à chaque tranche d'âge. Chez myMaxicours, nous croyons en une éducation où chaque élève trouve sa place, progresse à son rythme et développe sa confiance en soi dans un environnement bienveillant.

Profitez d'un accès direct à nos Profs en ligne pour une assistance personnalisée, ou explorez nos exercices et corrigés pour renforcer vos connaissances. Notre assistance scolaire en ligne est conçue pour vous accompagner à chaque étape de votre parcours éducatif, tandis que nos vidéos et fiches de cours offrent des explications claires et concises sur une multitude de sujets. Avec myMaxicours, avancez sereinement sur le chemin de la réussite scolaire, armé des meilleurs outils et du soutien de professionnels dédiés à votre épanouissement académique.

EXERCE-TOI EN T'ABONNANT