Comprendre la structure des graphes

Pour visualiser les liens entre les utilisateurs d’un même réseau social, on utilise des algorithmes qui agissent sur les bases de données. On arrive alors à élaborer des schémas, appelés graphes.

Exemple de modélisation d’un réseau social

• NSIbook est un réseau social qui comporte 7 membres :
  B, C, D, E, F, G et H.
• B est ami avec C, E et F.
• E est ami avec F.
• C est ami avec G et D.
• G est ami avec D.
• H est ami avec G et D.

Les membres sont entourés et la relation « être ami » est représentée par un segment qui relie les deux personnes qui sont amies.

Voici la représentation sagittale de ce réseau social.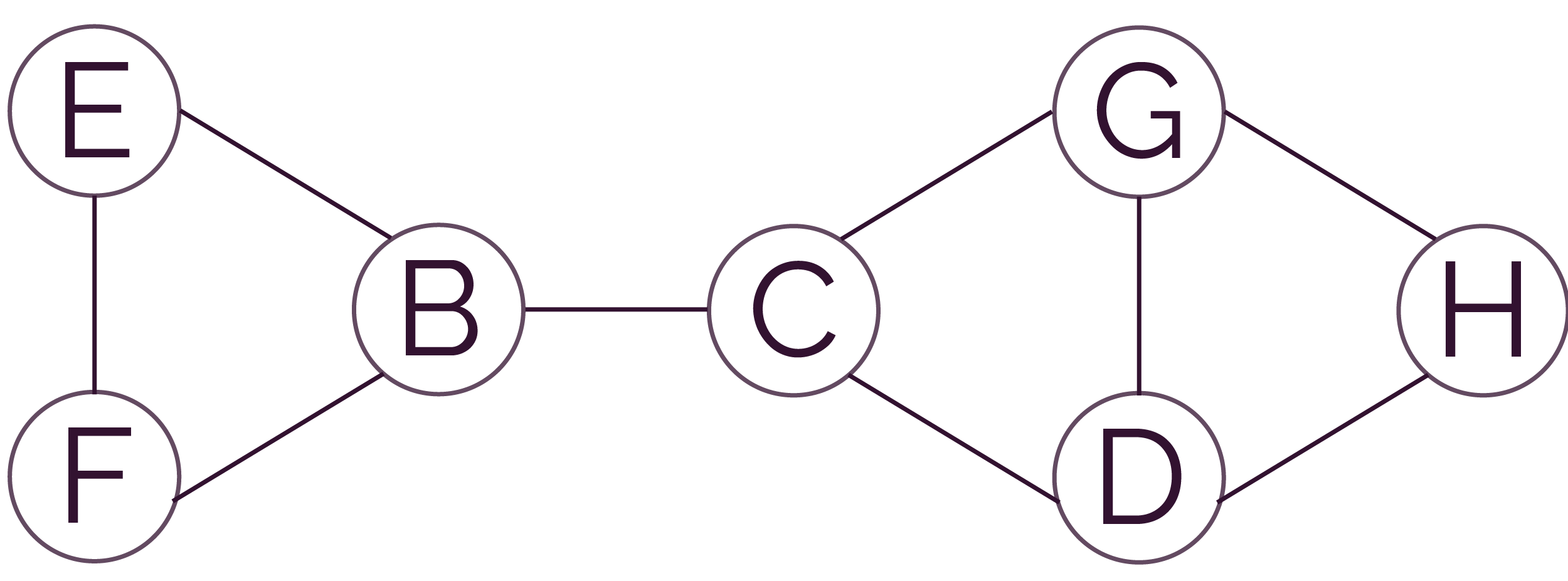

On peut modéliser bien d’autres situations réelles par des graphes (réseau routier, trajets, etc.). On peut ainsi définir une structure de données à partir d’un graphe.

On distingue deux types de graphes : non orienté et orienté.

Les arcs d’un graphe possèdent une extrémité initiale et une extrémité terminale.

Exemples

Graphe non orienté	Graphe orienté

Exemple
Dans le graphe orienté ci-dessous, la chaine est 1 – 3 – 2.

Un graphe possède les caractéristiques suivantes :

• la longueur d’une chaine est égale au nombre d’arêtes qui relient les sommets de cette chaine ;
• la distance entre deux sommets est égale à la longueur de la plus petite chaine qui les relie ;
• le diamètre entre deux sommets est égal à la longueur de la plus grande chaine qui les relie ;
• le centre d’un graphe est le sommet qui a la longueur la plus petite avec les autres sommets ;
• le rayon d’un graphe est égal à la plus petite longueur qui permet de relier le centre à tous les autres sommets.

Les caractéristiques d’un graphe

Exemple
Voici un exemple de graphe.

• La distance entre A et F est égale à 2 car le nombre minimum d’arêtes pour aller de A à F est de 2 (on passe de A à D puis de D à F).
• L’une des longueurs possibles entre A et F passe par C et E. Elle est égale à 3.
• Le diamètre est égal à 2 car la distance maximale entre deux sommets est de 2.
• Le centre du graphe est le sommet D car il a la plus petite distance avec les autres sommets.
• Le rayon du graphe est égal à 1 car il correspond à la plus petite longueur entre le centre D et tous les autres sommets.

On utilise le vocabulaire mathématique suivant, qui est associé à la théorie des graphes.

• L’ordre d’un graphe est le nombre de sommets du graphe.
• Deux sommets sont adjacents s’ils sont reliés entre eux par une arête.
• Le degré d’un sommet est le nombre d’arêtes issues de ce sommet.
• Un sommet qui n’est adjacent à aucun autre sommet du graphe est isolé.
• Un graphe est complet si deux sommets quelconques distincts sont toujours adjacents.
• Une chaine est une succession d’arêtes dont l’extrémité de l’une (sauf la dernière) est l’origine de la suivante.
  Le nombre d’arêtes qui composent une chaine est appelé longueur de la chaine.
• Une chaine fermée est une chaine dont l’origine et l’extrémité coïncident.
• Un cycle est une chaine fermée dont les arêtes sont toutes distinctes.

Exemple
Voici un exemple de graphe.

• Ce graphe est d’ordre 4 car il y a 4 sommets.
• B et C sont adjacents. C et A sont adjacents. C et D sont adjacents. A et D sont adjacents.
• B est de degré 1. C est de degré 3. A et D sont de degré 2.
• Il n’y a aucun sommet isolé.
• Ce graphe n’est pas complet puisque B et D ne sont pas adjacents.
• A – D – C est une chaine fermée, c'est donc un cycle.