Choisir une structure de données en fonction de la situation

Avant de se lancer dans l’écriture d’un programme, il faut se poser la question du choix de la structure de données : le but est de choisir une structure de données qui permette à l’algorithme d’être le plus efficace possible.

On va généralement retrouver des opérations dites usuelles comme la recherche d’un élément, un tri, etc.

Certaines structures sont plus adaptées que d’autres, en particulier lorsqu’on doit appliquer les mêmes opérations un très grand nombre de fois. Il faut donc parfois choisir un tableau plutôt qu’une liste, une pile plutôt qu’une liste, etc.

Pour pouvoir faire le bon choix, il faut étudier les différentes règles que les données doivent respecter. Avant de se lancer dans le choix, il faut lister ce dont on a besoin, c’est-à-dire déterminer les opérations (primitives) de la structure de données.

Si on a un doute entre deux structures de données, on peut implémenter les deux structures et faire des tests empiriques (sur des exemples bien choisis) sur la complexité temporelle.

• Une affectation est une procédure qui permet d’attribuer une valeur à une variable.
• Une comparaison est une instruction qui met en jeu deux variables et qui renvoie True ou False (vrai ou faux).
• Une opération est une instruction qui utilise +, –, *, /, //, % ou **.

On peut ainsi comparer ces structures de données et faire un choix.

On doit de plus pouvoir parcourir l'intégralité de la structure à l'aide de cette fonction successeur, sans passer deux fois par le même élément. Cela repose sur une notion que l’on nomme « liste chainée ».

La liste, la pile et la file sont des structures linéaires.

Exemple
Voici une pile qui représente les notes d’un élève.

On « empile » les notes.

Exemple
Voici une file qui représente les sites visités lors d’une navigation sur le web.

• La liste n'est pas adaptée pour accéder à un élément quelconque, car il faut la parcourir.
• La liste est intéressante si on doit supprimer ou insérer régulièrement des données.
• Si on doit ajouter ou retirer des éléments en tête de liste, on utilise la pile (car elle respecte le principe « dernier arrivé, premier sorti »).
• Si on doit insérer des éléments d'un côté et les retirer de l'autre, on utilise la file (car elle respecte le principe « premier entré, premier sorti »).

Voici la complexité temporelle de quelques opérations utilisées par les structures linéaires.

Un dictionnaire est une sorte de liste, mais au lieu d'être indexé, un dictionnaire utilise des clés : il s’agit de valeurs non mutables pour repérer et stocker des éléments appelés valeurs, qui peuvent être des nombres, des caractères mais aussi des p-uplets.

Les dictionnaires permettent de faire facilement des associations entre différents éléments. L’implémentation de cette structure de données se fait par l’intermédiaire d’une fonction de hachage (celle-ci permet d’accéder directement à la valeur).

Le dictionnaire est très efficace dans la recherche d’un élément à partir de sa clé, et dans l’insertion d’un couple du type (clé,élément).

Voici la complexité temporelle de quelques opérations utilisées par les dictionnaires.

Exemple
Le maximum correspond ici à la racine, donc à 4.

Les arbres équilibrés sont à privilégier pour :

• récupérer un maximum ou minimum (il suffit de regarder la racine) ;
• insérer d'un élément (il suffit de regarder les valeurs pour placer l’élément).

Voici la complexité temporelle de quelques opérations utilisées par les arbres binaires équilibrés.

Cette relation entre les deux enfants d’un nœud se retrouve de manière récursive à tous les nœuds de l’arbre.

Exemple
L’arbre suivant est un arbre binaire de recherche.

Le sous-arbre gauche de cet arbre est en effet le suivant.

C’est un ABR car la racine est 1 et on a :

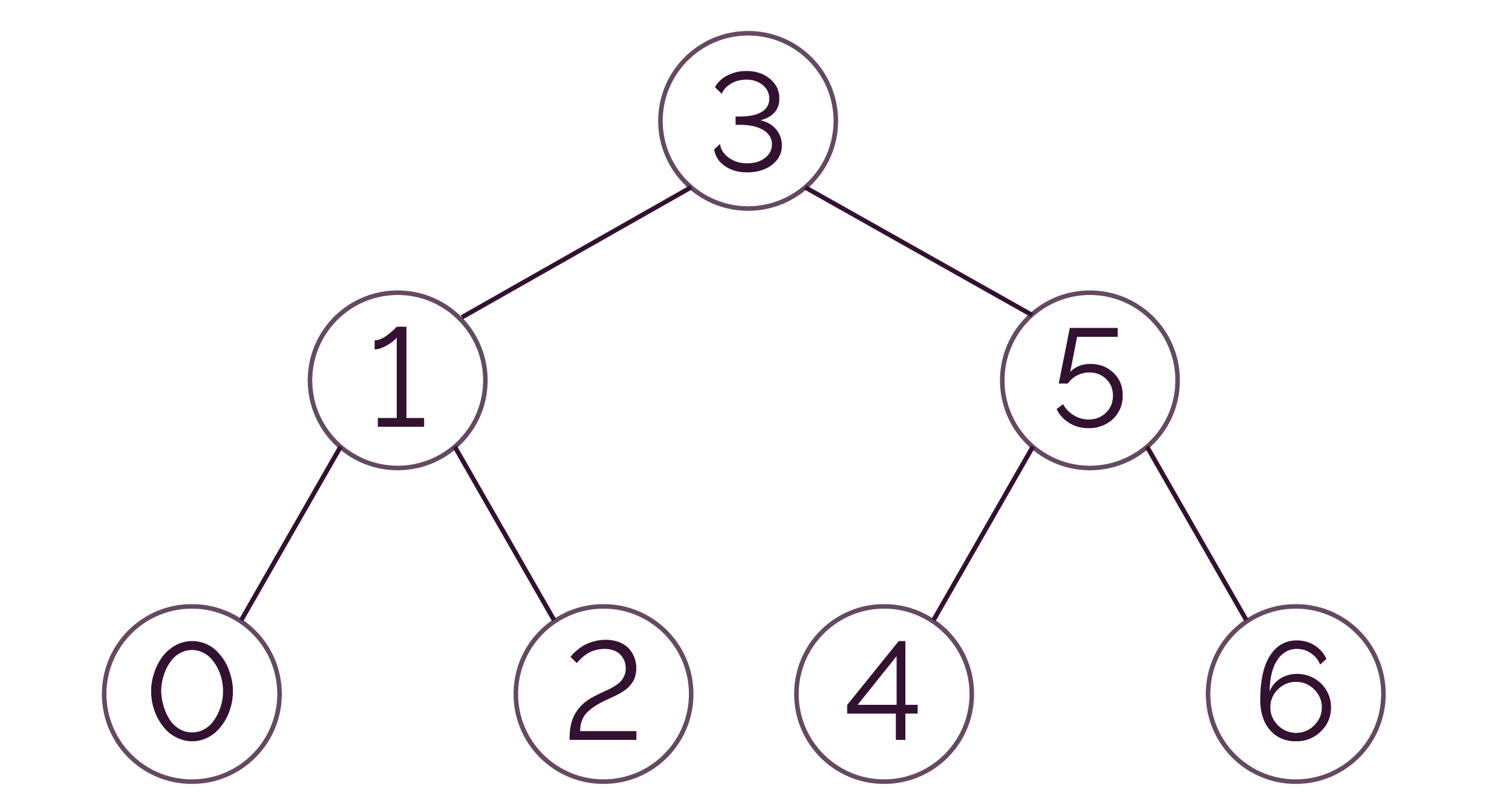
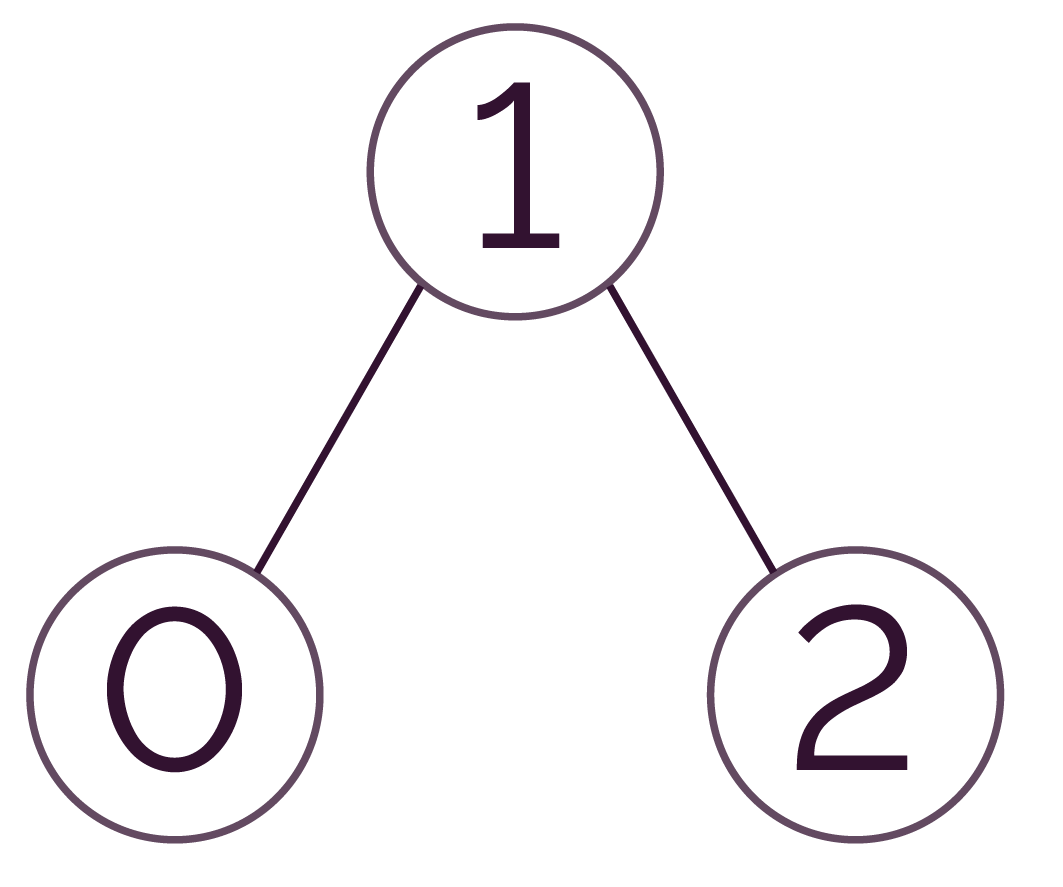
• à gauche : 0 ≤ racine :
• à droite : 2 > racine.

Également, le sous-arbre droit de cet arbre est le suivant.

C’est un ABR car la racine est 5 et on a :

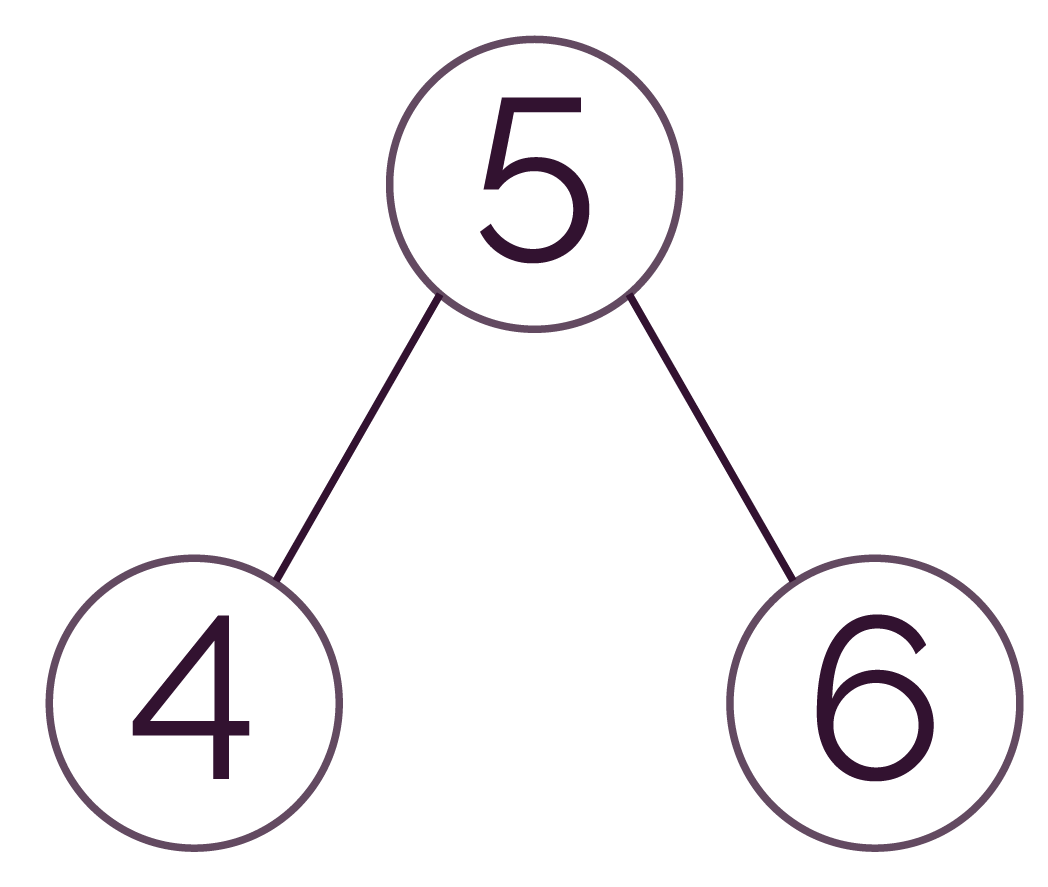
• à gauche : 4 ≤ racine ;
• à droite : 6 > racine.

Et enfin, si on considère 3, la racine de l’arbre, on a :

• à gauche : 1 ≤ racine (le fils gauche de la racine est inférieur ou égal à la racine) ;
• à droite : 5 > racine (le fils droit de la racine est supérieur à la racine).

Un arbre binaire de recherche permet de représenter une collection triée de données. On ne doit l’utiliser que pour des données qui sont comparables.

Cette structure de données est très utilisée pour rechercher et insérer des éléments dans un ensemble trié au préalable.

Voici la complexité temporelle de quelques opérations utilisées par les arbres binaires de recherche.